Ménage à trois sideral: los puntos de Lagrange

Los puntos de Lagrange (NASA)

(Actualización de las entradas publicadas en mayo de 2009.)

Escucha el podcast

Cuando pensamos en órbitas, imaginamos un cuerpo celeste describiendo un círculo o una elipse alrededor de otro. Ésta es la situación más simple, pero no es la única posible, ni mucho menos. Afortunadamente, en nuestro Sistema Solar los planetas están muy separados entre sí, y sus masas son muchísimo menores que la del Sol; por eso se mueven en órbitas elípticas alrededor de éste, y las perturbaciones que ejercen unos sobre otros son muy pequeñas. Y digo afortunadamente porque de esta manera las órbitas son muy estables. A efectos prácticos, se puede calcular el movimiento de cada planeta con bastante precisión considerando únicamente la atracción gravitatoria del Sol. Este problema es resoluble, y sus soluciones son las sencillas órbitas elípticas.

Pero en general, cuando hay más de dos cuerpos involucrados, el problema no se puede resolver analíticamente, y hay que recurrir a aproximaciones o a cálculos numéricos. Ni siquiera el llamado problema de los tres cuerpos, el que plantea el estudio del movimiento de tres cuerpos de cualquier masa sometidos a su atracción gravitatoria mutua, tiene una solución general que pueda expresarse con fórmulas matemáticas. Sí que la tiene un caso particular del problema de los tres cuerpos, el llamado problema de los tres cuerpos restringido circular, en el que se postula que la masa de uno de los cuerpos es despreciable respecto a la de los otros dos, y que éstos últimos tienen órbitas circulares; éste es el caso, por ejemplo, del sistema formado por la Tierra y la Luna y una nave espacial que se mueve entre ellas.

El problema de los tres cuerpos restringido circular tiene cinco soluciones estacionarias, cinco puntos en los que un objeto pequeño permanece en equilibrio estacionario respecto de los otros dos; son los llamados puntos de Lagrange o puntos de libración. El objeto, visto desde los dos cuerpos grandes, parece inmóvil en el cielo. Estos puntos de Lagrange se identifican con la letra L seguida de un número, desde 1 hasta 5.

El punto llamado L1 se sitúa entre los dos cuerpos grandes del sistema, en la recta que los une. Este punto es inestable: Si una pequeña perturbación acercare el objeto situado en L1 a uno de los cuerpos grandes, la atracción gravitatoria de éste aumentaría y apartaría aún más al objeto del punto de equilibrio.

En el sistema Sol-Tierra, L1 está situado a 1,5 millones de kilómetros de la Tierra en dirección al Sol, y es ideal para hacer observaciones de nuestra estrella. De hecho, alrededor de este punto orbitan tres observatorios solares: el Observatorio Solar y Heliosférico (SOHO), el Explorador de Composición Avanzado (ACE) y la sonda WIND.

En el sistema Tierra-Luna, el punto L1 sería muy adecuado para construir una base que sirviera de etapa intermedia para el transporte de personas y materiales entre nuestro planeta y su satélite.

El punto L2 está situado en la recta definida por los dos cuerpos grandes, como L1, pero más allá del más pequeño de los dos. Igual que L1, es inestable.

En el sistema Sol-Tierra, L2 está situado a 1,5 millones de kilómetros de la Tierra en la dirección opuesta al Sol, y es un buen lugar para situar un observatorio espacial. En este punto, la Tierra no llega a eclipsar por completo al Sol, el lugar vive en un eclipse anular continuo, pero el diseño y la operación del observatorio serían más fáciles porque éste mantendría continuamente la misma orientación respecto a la Tierra y el Sol. En este punto están situados la Sonda Wilkinson de Ani-sotropía de Microondas (WMAP), el observatorio Planck, el Observatorio Espacial Herschel y la sonda lunar china Chang’e 2.

En el punto L2 del sistema Tierra-Luna orbitan las sondas ARTEMIS P1 y ARTEMIS P2, que estudian la interacción de la Luna con el viento solar. Si un día nos decidimos a colonizar la Luna, allí se podría situar un satélite de comunicaciones para dar cobertura a su cara oculta.

Como los puntos L1 y L2 son inestables, las sondas espaciales situadas en ellos deben realizar regularmente correcciones de posición con sus motores para mantenerse allí.

El punto L3 es el recíproco de L2, y se sitúa también en la recta definida por los dos cuerpos grandes pero más allá del cuerpo más grande. Y también es inestable.

El punto L3 del sistema Sol-Tierra, situado al otro lado del Sol, fue en tiempos muy popular como ubicación de la “Anti-Tierra” en multitud de historias de ciencia ficción. La observación directa desde sondas espaciales ha mostrado que no hay ningún planeta allí.

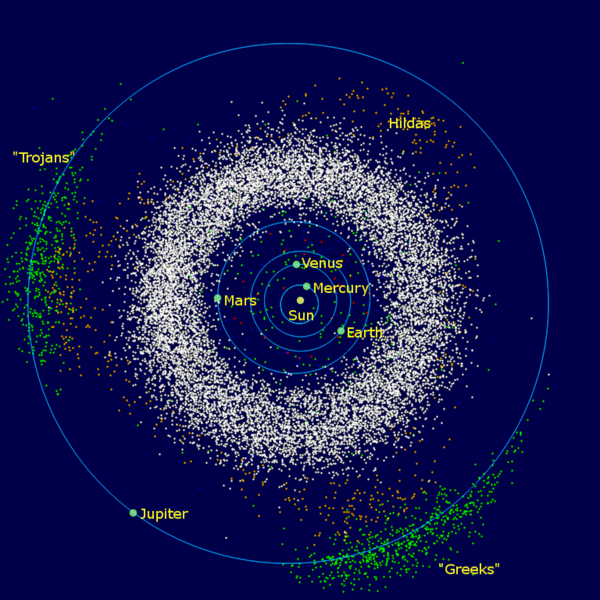Situación de los asteroides troyanos ("Trojans" y "Greeks") en el Sistema Solar
(Mdf, 2006)

Los puntos L4 y L5 corresponden al tercer vértice de los dos triángulos equiláteros situados en el plano de las órbitas de los dos cuerpos mayores y cuya base común es la recta que une dichos cuerpos. Vistos desde el cuerpo mayor, L4 precede al cuerpo menor en su órbita en un ángulo de 60º, mientras que L5 le sigue con ese mismo ángulo. L4 y L5 son estables, y en muchos casos existen objetos naturales situados en ellos. Estos objetos se denominan troyanos, por los nombres de los primeros asteroides de este tipo descubiertos, en los puntos L4 y L5 del sistema Sol-Júpiter.

En el sistema Tierra-Luna, los puntos L4 y L5 están ocupados por las nubes de Kordylewski, formadas por polvo interplanetario.

En el sistema Sol-Marte hay varios asteroides troyanos, como (5261) Eureka, situado en L5.

Los asteroides troyanos en sentido estricto son los que se encuentran en los puntos L4 y L5 del sistema Sol-Júpiter, bautizados con nombres de personajes de la Ilíada. Los asteroides del punto L5 llevan nombres de defensores de Troya, mientras que los del punto L4 llevan nombres de héroes griegos. Hay dos excepciones: (617) Patroclo, que es griego, está en el campo troyano, mientras que (624) Héctor, es troyano pero está en el campo griego.

El sistema formado por Saturno y su satélite Tetis tiene dos satélites troyanos: Telesto en L4 y Calipso en L5, al igual que el que forma el mismo Saturno con su satélite Dione, con Helena en L4 y Pollux (también llamado Polideuco) en L5.

En el punto L4 del sistema Sol-Neptuno hay varios asteroides, y también la Tierra tiene su propio troyano. Alrededor del punto L4 del sistema Sol-Tierra orbita el asteroide 2010 TK7, descubierto en octubre de 2010 y que aún no ha sido bautizado.

---